Isochrone

പണ്ട് തിലകൻ ചേട്ടൻ പറഞ്ഞപോലെ ലോകത്തിന്റെ സ്പന്ദനം കണക്കിലാണ് describe ചെയ്തിരിക്കുന്നത് . തിലകൻ ചേട്ടൻ ഉദ്ദേശിച്ചത് എന്താണെന്നാണ് explain ചെയ്യുകയാണ് ഈ ബ്ലോഗ്. പിന്നെ കണക്കില്ലെങ്കില് ഭൂഗോളം ഒരു വട്ടപ്പൂജയമൊന്നും ആകില്ല കാരണം കണക്കില്ലെങ്കില് പിന്നെവിടുന്നു വട്ടപ്പൂജ്യം . സ്പന്ദനങ്ങളെക്കുറിച്ച് കണക്കിന്റെ ഭാഷയിൽ എഴുതാന് ഉപയോഗിക്കുന്ന ഒരു ടൂള് ആണ് ഡിഫറൻഷ്യൽ equations.

നമ്മളുടെ ഹാർട്ട് , ബ്രെയിൻ പിന്നെ കടലിലെ തിരമാല അങ്ങനെ എല്ലാത്തിലും ഈ ഓസിലേഷൻസ് കാണാൻ പറ്റും . പൊതുവേ ഈ സ്പന്ദനങ്ങള് (ആന്ദോളങ്ങള് ) 2 തരമാണ് ഉള്ളത് 1.അതിനെ ചെറുതായി perturb ചെയ്താല് തിരിച്ചു പഴയപോലെ ആകുന്നവ 2. അല്ലാത്തവ. ഇതിൽ ആദ്യത്തെ ടൈപ് ആണ് ഞാന് ഇവിടെ പറയാൻ പോകുന്നത്… പ്രകൃതിയില് പൊതുവേ അങ്ങനെയുള്ളതാണ് കാണുക എന്നാണ് എനിക്കു തോന്നുന്നത് . അത്തരം ആന്ദോളനങ്ങൾ സൃഷ്ടിക്കുന്നതിന് ഡിഫറൻഷ്യൽ സമവാക്യ സംവിധാനം ‘പരിധി ചക്രങ്ങൾ’(Limit cycle translated by google ) ഉണ്ടാക്കേണ്ടതുണ്ട്. ഉദാഹരണത്തിന് ഒരു ഡിഫറൻഷ്യൽ സമവാക്യത്തിൽ രണ്ട് സ്റ്റേറ്റ് വേരിയബിളുകൾ ഉണ്ടെന്ന് പറയാം. ഇതിനെ x, y എന്ന് വിളിക്കാം. സമയം പുരോഗമിക്കുമ്പോൾ ഈ വേരിയബിളുകൾ മാറിക്കൊണ്ടിരിക്കും. അവ ‘പരിധിചക്രങ്ങൾ’ സൃഷ്ടിക്കുമ്പോൾ, താഴെ കാണിച്ചിരിക്കുന്നതുപോലെ അവ ആ സ്ഥലത്ത് ഒരു വൃത്താകൃതിയിലുള്ള ഫാഷനിൽ പോകുന്നു. അതിന്റെ സ്റ്റാർട്ടിങ് പോയിന്റ് പരിധി-ചക്രങ്ങളുടെ അടുത്ത് നിന്നാണ് തുടങ്ങുന്നതെങ്കിൽ, ആ ഫ്ലോ അതിലോട്ട് അസ്മിപ്റ്റോട്ടിക്ക് ആയി ആകർഷിക്കപ്പെടും. 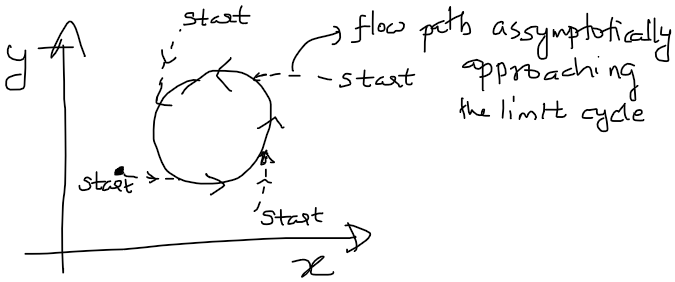പരിധിചക്രത്തിലെ ഒരു പോയിന്റിനെ നമുക്ക് എല്ലായ്പ്പോഴും ഉത്ഭവസ്ഥാനം O ആയി നിരവചിക്കാൻ കഴിയും. അങ്ങനെ ചെയ്തു കഴിഞ്ഞാല്, പരിധിചക്രത്തിലെ മറ്റുള്ള പോയിന്റ് കളുടെ phase നമുക്ക് നിരവചിക്കാൻ സാധിക്കും. ആതിപപ്രകാരമാണ്, ആ പോയിന്റില് നിന്നു ഉദ്ഭവ സ്ഥാനത്തേക്ക് എത്രനേരം ട്രാവെൽ ചെയ്താല് നമ്മള് ഉദ്ഭവസ്ഥാനത്ത് എത്തുമോ അതാണ് ആ പോയിന്റിന്റെ phase. അതിനുശേഷം xy planeനിൽ ഉള്ള ലിമിറ്റ് സൈക്കിളിന്റെ അടുത്തുള്ള മറ്റുള്ള പോയിന്റ് കളുടെ phase നമുക്ക് ഈസീ ആയി നിരവചിക്കാം. കാരണം asymptotically അടുത്തുള്ള എല്ലാ പോയിന്റകളും limit സൈക്കിൾ ഇൽ വന്നു വീഴുമല്ലോ. ആപ്പോള് അതിലെ ഒരു പോയിന്റും ലിമിറ്റ് സൈക്കിൾ ന്നു പുറത്തുള്ള ഒരു പോയിന്റും asymptotically ഒരേ സമയം ഉദ്ഭവ സ്ഥാനത്ത് എത്തും. അപ്പോള് നമുക്ക് ആ പുറത്തുള്ള പോയിന്റ് ന്റെ phase ലിമിറ്റ് സൈക്കിൾ ഇൽ ഉള്ള മറ്റെ പോയിന്റ് ന്റെ phase നോട് equate ചെയ്യാം. അങ്ങനെ നമുക്ക് എല്ലാ xy plane ഇൽ ഉള്ള point ന്റെയും phase കിട്ടും (പരിധിചക്രത്തിനാടുത്തുള്ള എല്ലാ pointന്റെയും). ഒരേ phase ഇൽ ഉള്ള എല്ലാ പോയിന്റുകളും ഒരു isochron ഇൽ വരും. 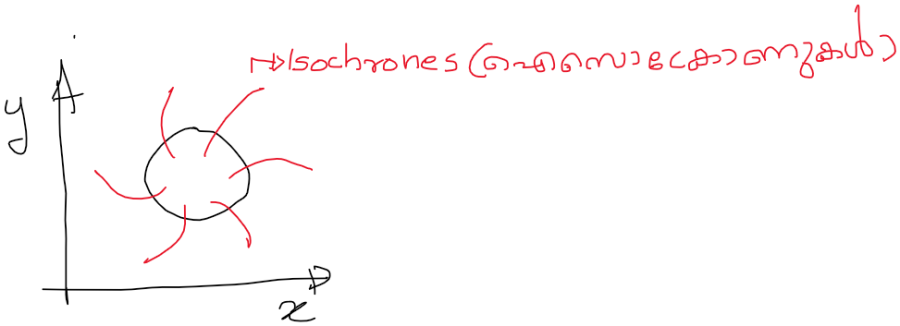ഇതൊക്കെ എന്തിനാണ് ഉപയോഗിക്കുന്നത് എന്നു വേറൊരു ബ്ലോഗില് പറയാം. ബൈ ബൈ.

Posts

subscribe via RSS